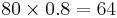Discounted maximum loss
Discounted maximum loss is the present value of the worst case scenario for a financial portfolio.
An investor must consider all possible alternatives for the value of his investment. How he weights the different alternatives is a matter of preference. One might require a pension fund never to go bankrupt. If this is the case, the manager of its portfolio must consider the worst alternative as the benchmark. Finally, as the investment takes place today he must evaluate the alternatives in their present value, hence the discounting.
Definition
Given a finite state space  , let
, let  be a portfolio with payoff
be a portfolio with payoff 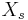 for
for 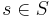 . If
. If 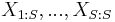 is the order statistic the maximum loss is simply
is the order statistic the maximum loss is simply 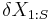 , where
, where  is the discount factor.
is the discount factor.
Properties
The Discounted maximum loss is the 1-expected shortfall. It is therefore a coherent risk measure.
Example
As an example, assume that a portfolio is currently worth 100, and the discount factor is 0.8 (corresponding to an interest rate of 25%):
| probability | value |
|---|---|
| of event | of the portfolio |
| 40% | 110 |
| 30% | 70 |
| 20% | 150 |
| 10% | 20 |
In this case the maximum loss is from 100 to 20 = 80, so the discounted maximum loss is simply